Floquet & Heating

In Plain English

To deepen our understanding of various phenomena we often seek to find very controllable and clean model systems that should be able to capture the main physics of the relevant problem while allowing a theoretical description and a simple experimental realisation.

Cold gas systems are clouds of atoms that are cooled to extremely low temperatures such that their quantum nature becomes important. These systems allow very precise control and measurement of many of their properties and can be used to simulate a variety of physical systems.

One interesting approach is to expose these systems to time-varying light fields to be able to simulate the effect of magnetic (and more general) fields. In some sense this corresponds to “shaking” the atoms. Thus, one would expect that this procedure possibly injects energy into the system, heating it, or allows the atoms to be excited. Usually, one would like the system not to be heated up and to remain cool. Therefore, a theoretical understanding of these heating processes and prescriptions how to keep the good effects of the shaking while minimising the bad heating are required.

Research

This work is mostly focussed on systems of cold atomic gases. It is motivated by recent experimental developments, in particular the time-modulated tuning of system parameters in cold gas set-ups. It explores the novel aspects arising in these quantum many-body systems focussing on both time-dependent effects and collective many-body phases. The basic question is what new phenomena arrise from the interplay of time-dependence and the presence of interactions.

Scattering Theory

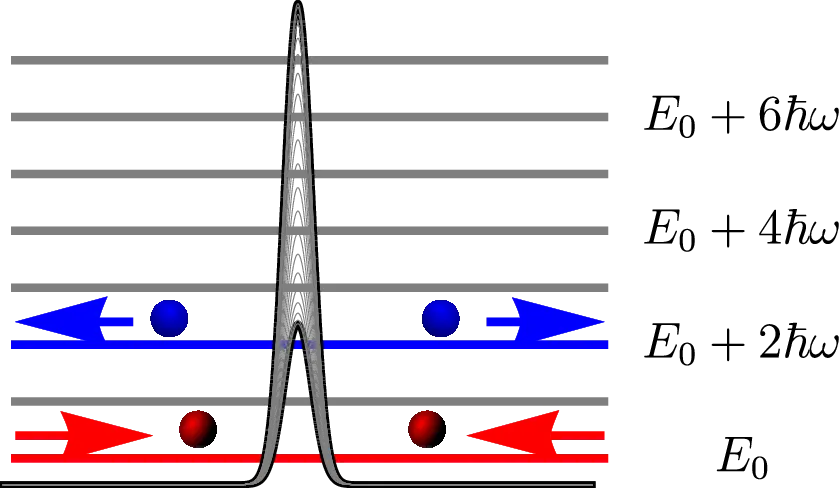
I developed a framework to perturbatively include the effects of interactions in time-periodically driven systems, particularly studying them in the context of the generation of artificial gauge fields for cold atoms. The relevant framework for the treatment of time-periodic Hamiltonians is Floquet Theory. Due to the breaking of time-translation invariance energy is not conserved, but the time-periodicity of the Hamiltonian rather only ensures the conservation of quasi-energy. This in turn implies that particles can absorb or emit quanta of energy \( \hbar \omega \) during scattering.

Population Dynamics

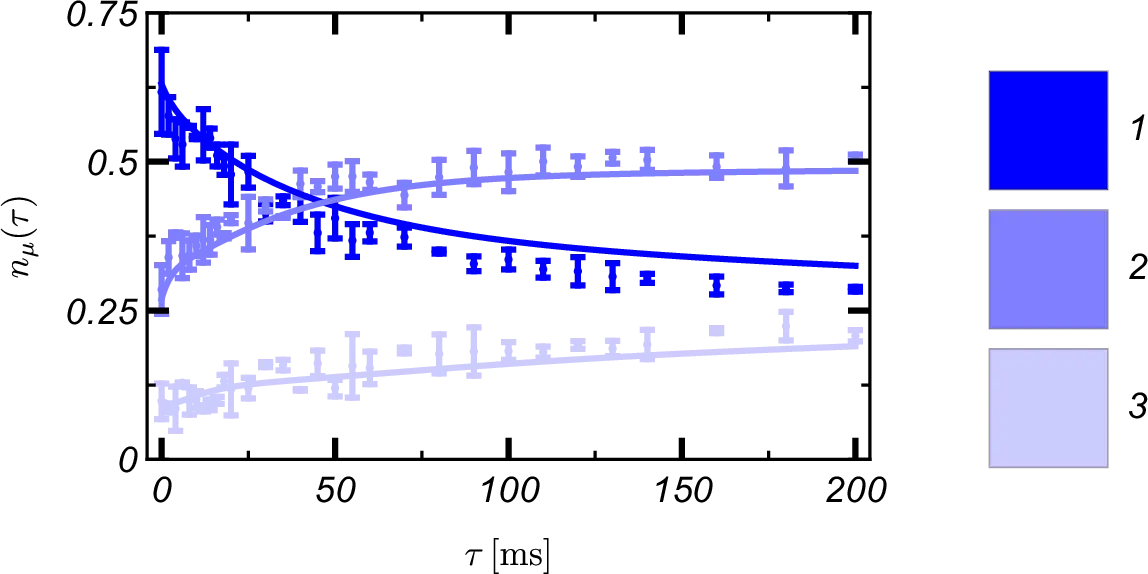
I have explored the consequences of these novel interaction effects in time-periodically driven quantum systems. I consider both generic model systems and the experimentally relevant realisation of the Harper-Hofstadter Hamiltonian in terms of the competition between elastic scattering, required for correlated many-body phases, and inelastic scattering, leading to deleterious heating and particle loss. I obtained results for the population dynamics in good agreement with the experimentally observed data.