Chaos & Butterfly effect

In Plain English

Chaos is one of the fields of physics which has widely entered into the public's imagination.

Perhaps, the best known manifestation of chaos is the butterfly effect: The idea that a slight perturbation, the literal beating of a butterfly's wings in one part of the world, can have dramatic effects on the dynamics, and cause a tornado at the other end of the world.

There are two aspects to this effect, one is the extreme sensitivity to slight changes in initial conditions (presence/absence of a butterfly's wing beat), the other is the spatial separation between cause (wingbeat) and effect (tornado). The first is formally captured by what is called a Lyapunov exponent, measuring how fast a slight change grows (exponentially) in time, whereas the second requires a spreading of the change from the initial cause to the effect, which is captured by the butterfly speed.

Generically, not only weather systems are expected to show such chaotic behaviour, but rather any (sufficiently) complicated system of many constituents.

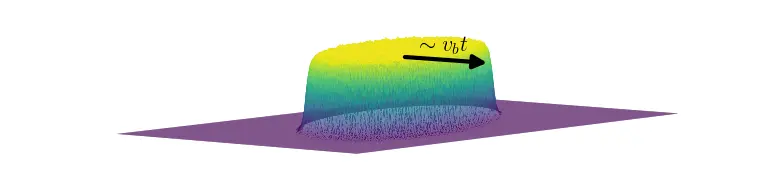
In this work we study the above effect in a system of spins (~arrows) sitting on the points of a two-dimensional lattice, called the Kagome lattice (see image below). Also here, we find that an intially local change (in the centre of the system) spreads through the system and grows exponentially in time (see the videos below and image to the right).

Research

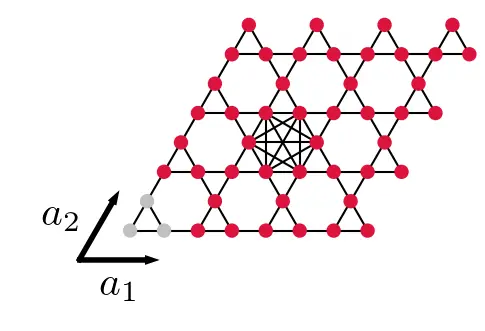
At the heart of this project is the interplay of geometric frustration, dynamics and chaos in a classical many-body spin system on the Kagome lattice.

In the studied model the spin liquid phase extends all the way down to zero temperature which allows us to trace the markers of many-body chaos as characterised by the butterfly effect of out-of-time-ordered correlators (OTOC) over the whole temperature range.

We obtain the temperature dependence of the butterfly speed and Lyapunov exponent and find novel algebraic scalings of these quantities, in seeming violation of quantum bounds on chaos, but compatible with recently suggested relations between these measures of microscopic chaos and common measures of macroscopic transport, such as spin diffusion.

Our study of chaotic dynamics in a 2-dimensional classical many-body spin system has implications for the classical-quantum correspondence, the relevance of OTOC’s in classical chaos, and the relation of microscopic chaos to macroscopic transport.

Dynamics of the OTOC

The videos show the dynamics of the OTOC at different temperatures, one at high temperature (T=100, left) characteristic for the uncorrelated trivial paramagnetic state, and one at low temperature (T=0.1, right), characteristic of the spin-liquid state.

We observe isotropic ballistic spreading of the perturbation for all temperatures. In addition, we observe that with decreasing temperature the butterfly speed decreases, as propagation of the wavefront slows down, as well as a decrease of the Lyapunov exponent, visible in the longer time required for the build-up of a wavefront.