SU(N) Fermi Gases

In Plain English

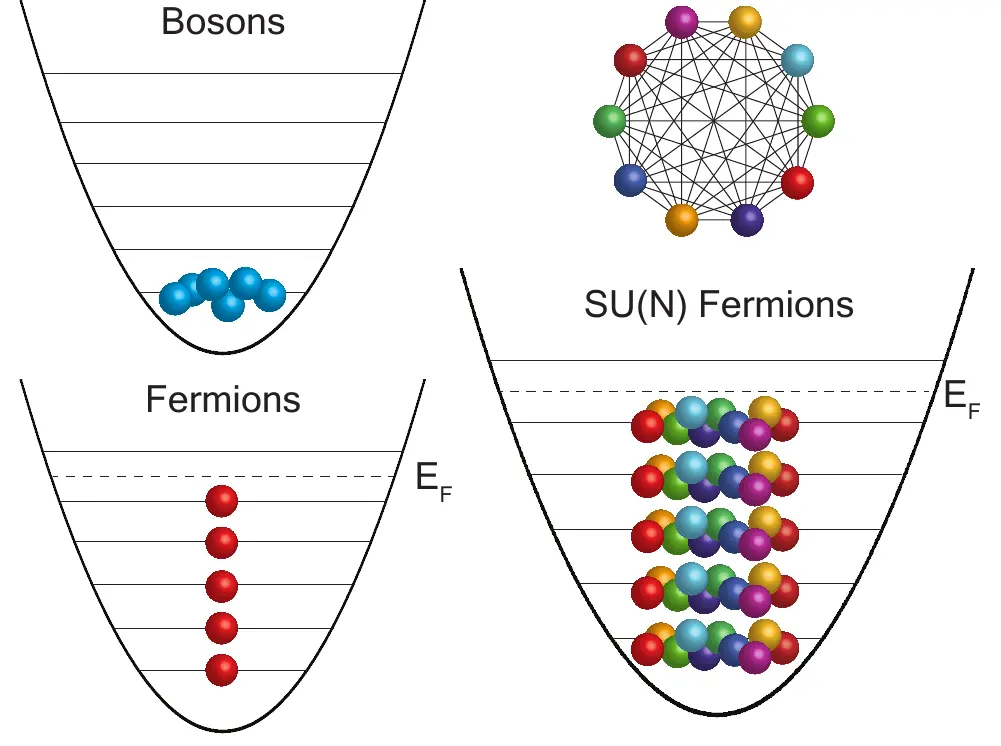
At the foundation of our understanding of modern physics lie the symmetries realised in nature.

Perhaps, surprisingly, real systems, here atomic gases cooled down to very low temperatures, can pristinely realise rather symmetry groups. Here, we study a gas with N distinct states, which due to the symmetry all behave in the same fashion, e.g. they are SU(N) symmetric.

In particular, they all feel the same interactions between each other, and the interplay between the interactions and this large symmetry, is what results in exciting physics in this system.

Also have a look at the popular summary in the JILA News

Research

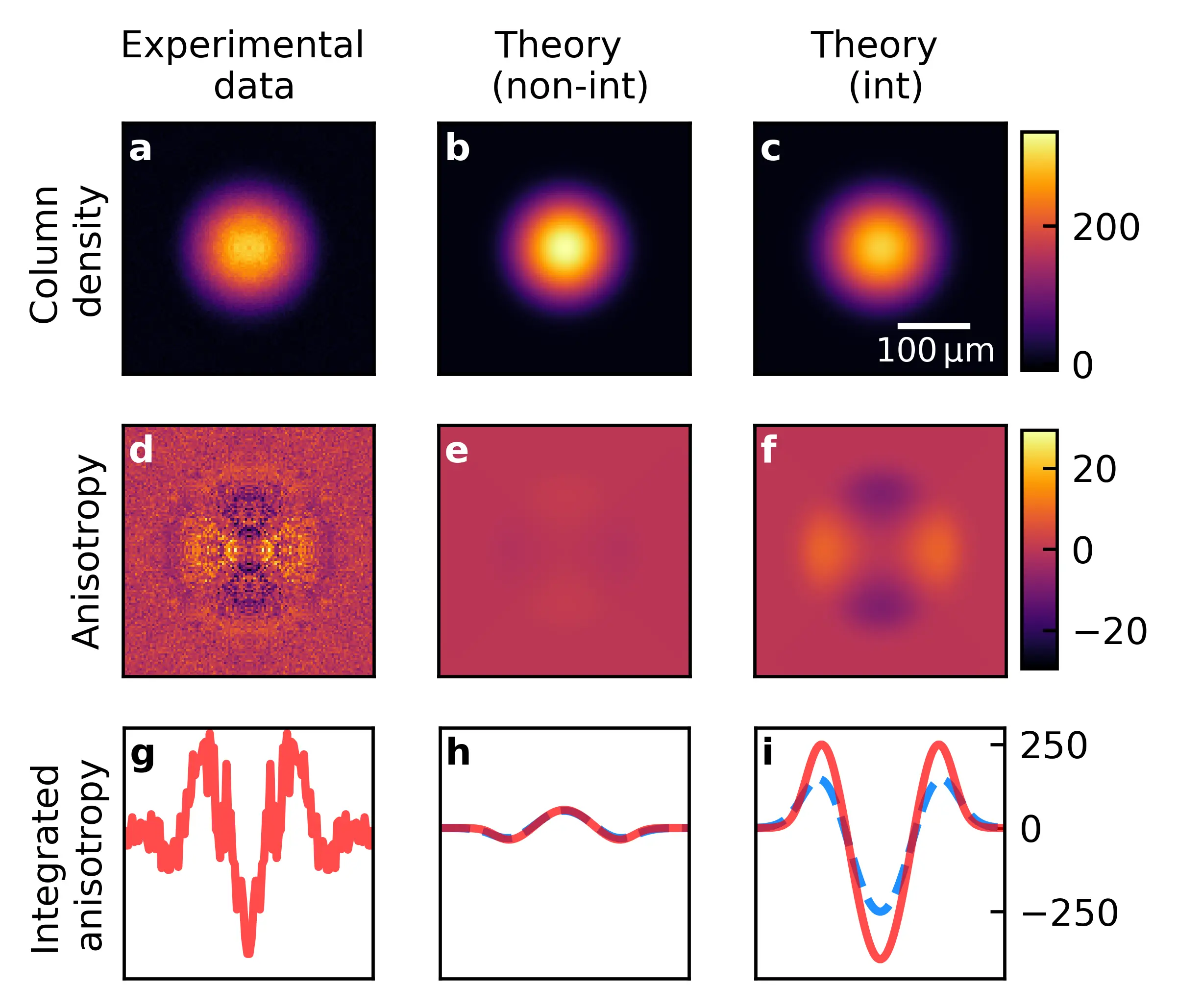
The motivation for this project is to understand the relevance of SU(N) interactions on the thermodynamics and expansion dynamics of an ultra-cold gas of Sr as realised here in the labs at Jila in the group of Jun Ye.

The SU(N) symmetry of the interactions in this system results in an increased strength of the interactions by a factor of the available scattering partners, N-1. This allows to study and experimentally observe interaction effects in a nominally weakly interacting system.

We characterise the thermodynamic behaviour of this system via the compressibility which is directly related to the observed number fluctuations, which we find to be strongly suppressed indicating the relevance of interactions and degeneracy pressure in this interacting quantum system. We further study the importance of the interactions on the time-of-flight dynamics, a standard tool for extracting information on the gas. We use the Boltzmann-Vlasov equation to theoretically compute in-situ and time-of-flight phase-space distributions of the interacting gas, which allows us to accurately predict the experimentally observed behaviour.

In the broader context, the understanding and characterisation of SU(N) quantum matter is an important step towards realising the novel phases predicted when these systems are confined in lattice geometries.

Time-of-flight expansion dynamics

These videos compare the density distribution (integrated along one axis) after time-of-flight comparing a non-interacting Fermi gas, and the interacting SU(N) Fermi gas during expansion from an initially anisotropic trapping potential.

In the non-interacting gas at long times the density distribution corresponds to the initial momentum distribution which even in an anisotropic trap is isotropic. However, in presence of interactions, we predict and observe an inversion of the initial spatial anisotropy. This effect even allows us to make the presence of interactions visible by analyising a single experimental image and the contrast/asymmetry of these distributions present due to the interactions.