Disorder & Flat Bands

In Plain English

At the heart of this project is the interplay of geometry & frustration, topology and disorder on the Kagome lattice.

The Kagome lattice is an interesting type of lattice, a regular arrangements of points in the plane, which displays strong frustration.
Frustration shows itself in many ways: In this case we are considering particles moving on the Kagome lattice. It turns out that there are a large number of states/ways particles can do this at exactly the same energy.
Now, to connect this with frustration, all these states having the same energy suppresses ordering as the system cannot "choose"/order into just any of them.

These states have the interesting property that one can choose them to be local. i.e. the particles in spite of being able to move everywhere, in fact stay in a small region. This is an effect of destructive interference of different paths of a quantum particle relying on exact cancellation.

The research question now is whether this situation is very special requiring fine-tuning or stable to small changes of the system such as disorder. Naively, it seems implausible that it could ever be stable since any small change should change the energies a bit. However, there is a way out which physicists call topological protection, which describes exactly properties that are in some sense stable to suitable changes of the system.

Research

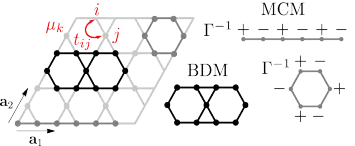
We study two models of correlated bond- and site-disorder on the kagome lattice considering both translationally invariant and completely disordered systems. The models are shown to exhibit a perfectly flat ground state band in the presence of disorder for which we provide exact analytic solutions. Whereas in one model the flat band remains gapped and touches the dispersive band, the other model has a finite gap, demonstrating that the band touching is not protected by topology alone. Our model also displays fully saturated ferromagnetic groundstates in the presence of repulsive interactions, an example of disordered flat band ferromagnetism.