Chaos & Phase Transitions

In Plain English

Chaos is one of the fields of physics which has widely entered into the public's imagination.

Perhaps, the best known manifestation of chaos is the butterfly effect: The idea that a slight perturbation, the literal beating of a butterfly's wings in one part of the world, can have dramatic effects on the dynamics, and cause a tornado at the other end of the world.

There are two aspects to this effect, one is the extreme sensitivity to slight changes in initial conditions (presence/absence of a butterfly's wing beat), the other is the spatial separation between cause (wingbeat) and effect (tornado). The first is formally captured by what is called a Lyapunov exponent, measuring how fast a slight change grows (exponentially) in time, whereas the second requires a spreading of the change from the initial cause to the effect, which is captured by the butterfly speed.

At the same time we are used to classical systems and the world around us to show order and structure. Water freezes at low temperature and becomes ice. This transition from one phase to another, water/ice, is called a phase transition in physics. Typically at lower temperatures things appear more ordered. One might now wonder what happens to the butterfly effect and chaos once a system undergoes such a transition from a disordered state like water to a highly ordered state like ice. Does the system still show chaotic behaviour, or does chaos fundamentally change across a phase transition?

In this work we study the above effect in a system of spins (~arrows) sitting on the points of cubic lattices, e.g. 1D chains, 2D square lattices, and 3D cubic lattices. These system order at low temperature in the sense that neighbouring spins either align or anti-align, just as you are used to from magnets.

Research

At the heart of this project is the interplay of dynamics, order and chaos as a spin system crosses the phase-transition from a high temperature paramagnetic state to a low-temperature ordered state.

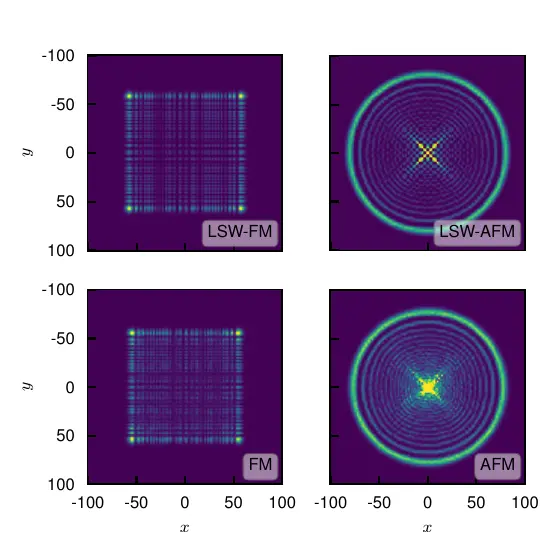
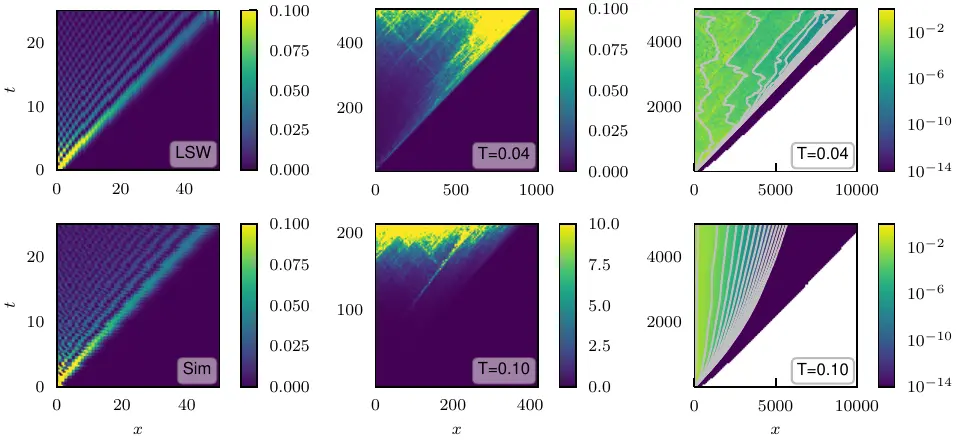
We study the behaviour of the decorrelator and butterfly effect in classical Heisenberg (anti-) ferromagnets on non-frustrated cubic lattices in one, two and three dimensions. While the three-dimensional model shows a proper thermal phase transition into an ordered phase, even one and two dimensions show at least a finite system size transition, which allows us to investigate the effects of broken symmetries, global order and emergence of quasi-particles on many-body chaos

We find three distinct regimes in the behaviour of the decorrelator. At short times and temperatures deep in the ordered phase we observe an integrable regime, well described by spin-wave physics. This crosses over into a scarred regime, in which rare scattering events of ballistically propagating quasi-particles dominate the decorrelator. This finally gives way to long-time exponential growth and chaos as scattering events proliferate.